After a gazillion hours of procrastination, I'm finally writing it. It's a topic that's very important for paleontologists and biologists (amateur or professional alike), and yet a lot of universities outright fail to teach it, especially at the undergraduate level. What am I talking about?
Of course, I'm gonna be talking about
lies, damned lies, and statistics.
There's a reason it took me so long to write this. Statistics are freaking hard. There's a reason why I didn't major in math, even if I find the subject as such cool.
Unfortunately, there's no way I'll be able to cover this in under six thousand words. It's not that long (many of IB's retrospective reviews are longer), but it's longer than the usual tutorial in this thread, so better grab a book (on math) as I walk you through it.
Keep in mind that a lot of this guide covers entry-level stuff, so if you studied anything quantitative, you might not learn much new. Even so, I think the last two sections discuss topics that occasionally confuse even pros.
Without further ado, this is what we'll concern ourselves with.
Table of Contents:
1. What is Statistics?
2. Biology as a Hypothesis-Driven Science
3. Raw Data Analysis
4. Statistical Modelling
5. Why Correlation Does Not Prove Causation
6. What's the Point of All of This?1. What is Statistics?Biology is sorta unique among the big three of the natural scientists. Unlike physicists or chemists, we kinda suck at math. We don't have fancy equations that model the orbit of planets around the Sun, nor do we have to do equilibrium concentrations of our solutions.
Biology doesn't concern itself with underlying mathematical principles. It concerns itself with
populations.
I'm not talking about the biological meaning of a subset of a species that is geographically and ecologically connected. For the purpose of this guide, a "population" is a set of data points grouped based on commonality. Such data points can be anything. The stars in the sky, the hairs on a head, the number of coins you flipped, anything.
Sometimes, population sizes can be small and handy. But sometimes, they can also be overwhelmingly huge. If you are dealing with the stars in the sky, you will have a hard time making statements that apply to all of them.
It's easy to make statements about a population. Simply count their members and attributes you wish to measure and put them in a table. If you're dealing with coin flips, a table might look like this:
| Flips | Result |
| 1 | Tails |
| 2 | Heads |
| 3 | Tails |
| 4 | Heads |
| 5 | Tails |
| 6 | Tails |
Now, six coinflips aren't much. What if you have a larger - much larger - sample size, like the stars in the sky? Surely you can't count them all?
Say, you're a quality control manager. Products are being produced (food, drugs, you name it) and you need to assess how good they are. Problem is, you cannot check them all.
If you were to control the quality of bread, it'd be impractical to take a bite out of all the products (after all, the consumer needs something). Instead, you take a representative sample (ideally from every class of bread you'd like to test) and extrapolate the results on the rest. If you got ten random pieces of bread and they all made you vomit, it's unlikely the rest is any good either!
Again, for the record so that you guys can take notes.
Our goal in statistics is to extrapolate results from a sample to the population it was taken from.In biology/paleontology, we are faced with the problem of limited data all the time. How do we know the average mass of
Tyrannosaurus if we don't even have a hundred specimens? How do we know the mean prey size of polar bears if most of their hunts happen while we aren't watching? And how can we test the effects of medication on high blood pressure without harming the entire American population if our medication turns out to be bad?
Let's say we have such a dataset.
What do we do first?
I initially wanted to write an entire chapter about the mean, the median, and standard deviations, but I decided to push it further back.
For one, it's pretty boring and technical.
For another, you nowadays have statistics software to calculate that for you.
Data is meaningless without someone who knows how to interpret it.
The first thing we do is to
formulate a hypothesis.
2. Biology as a Hypothesis-Driven ScienceA thing I always find interesting is how different professionals tend to solve problems in different ways. Some mathematicians or computer scientists, for example, like to look at a bunch of data and are perfectly willing to play around with the prettiest models they can find and any hypothesis comes later.
As biologists or paleontologists, we aren't like that. The things that interest us most are questions.
The paleo people probably know what I'm talking about, as we, unfortunately, have far more questions than useful data in that space.
So, we start with a question. How big was
O. megalodon? How big was the mean size of theropod species X of which you only have a hundred specimens?
With the limited data, we have from the fossil record, we can't really "prove" anything, but that's okay. Karl Popper said you don't have to prove a hypothesis right, you only have to prove it wrong.
"But I don't want to prove my hypothesis wrong, I want to prove it right!"
There's a simple solution: Simply assume the opposite of what you are trying to prove (the null hypothesis) and then disprove it!
The null hypothesis is usually a statement of insignificance. If your hypothesis is something like "All swans are white", the null hypothesis would be "Not all swans are white". If this null hypothesis was true, you'd at some point in your life expect to observe a swan that isn't white. If you never do, there's a good chance that the hypothesis is wrong and all swans are indeed white.
"But what if there are non-white swans and I just never see them?"
Excellent questions.
This is where statistics come into play.The truth is, we can't prove with 100% certainty that there are no non-white swans, but we don't need to.
Statistics is about probabilities, not 100% certainties. 99.99999% might not be as good as 100%, but, come on, it's close enough.
How do we compute probability though?
Weeeeeellllll, I'm glad that you asked. See, I wanted to explain it in this section, but it's not easy. Why not let me walk you through the entire field of statistics first?
3. Raw Data AnalysisWhen we have a hypothesis, we need data. Data means samples from your population (see above). If you want to evaluate the average adult body length of an extinct theropod which is known from a hundred adult specimens (a lot by paleontological standards, but very little compared to how many adult specimens actually lived), this is your sample data right here.
When you have a dataset, you first need to characterize it before you can do any kind of analysis on it whatsoever. The first and most important questions: Is your data
continuous or
categorical?
Categorical data occurs when, you guessed it, we can neatly classify our data point into categories and
continuous data occurs when you can't. Let's say we want to determine the gender of our theropods. We only really have two options, male or female, so that's categorical data right there, but when we want to measure their length, then, assuming they are T. rex-sized the value we get could be anything between 0 and 13 m, so that's continuous. Right?
Not so fast! Intersexuality exists in the animal kingdom, so who's to say there weren't some (very rare) hermaphrodites among our theropods?
And sure, length might appear continuous, but we can't measure it to an infinite degree of accuracy, so, if we just go down enough decimal places, it might become categorical again, won't it?
Very true. Mathematicians have extremely formal definitions of what words like "continuous" and "categorical" mean. However, I'll tell you a secret. Mathematics is a science that works on definition, not on description. Therefore, mathematicians can stay in their ivory tower and leave us alone. We, who deal in the real world, sometimes have to dumb things down and simplify things. Yes, some animals have infertile, intersex hybrids, but they're so rare that we can ignore them for the sake of our studies. Likewise, we can't measure an animal's length with infinite accuracy, but three significant digits are still good, aren't they?
(Some statisticians also have a third category,
discrete, which is data points that are intermediate between continuous and categorical. Say, the size of a fish swarm. We can't easily categorize it, as sizes vary too wildly, but it's not infinitely continuous either, as no swarm can have 21321.432423 fish or anything. But I can see that your head is already smoking, so I'll leave it at that.)
Besides determining the data type, we can characterize it in other ways. A good way to characterize the data set is by finding out its average value. Sometimes, finding the average is the goal in and of itself, as it is in our example.
There are, broadly speaking, three ways of determining the average of a data set and they are called
MMM:
Mode,
median, and
mean.
The
mode is the most common value. In the dataset [2, 12, 12, 19, 19, 20, 20, 20, 25], 20 is the mode, as it appears three times (2 and 25 appear once, 12 and 19 appear twice).
The
median is the value that lies at the center of the data set if you rank the data from smallest to biggest. Our previous dataset ([2, 12, 12, 19, 19, 20, 20, 20, 25]) has nine entries. The middle entry of these would be the fifth column, so, in other words, 19. Okay, what if it has an even number of entries? [2, 12, 12, 19, 19, 20, 20, 20, 25, 25] Here, we have ten entries. The median would be between the fifth and sixth entry (19 and 20) and the middle of these is 19.5.
How about the
mean? This one is difficult to explain for two reasons.
1) It involves far more math than the other two.
2) There's many, many ways to compute the mean.
Common types of means are the arithmetic mean, the geometric mean, the harmonic mean, and the weighted mean. However, in my opinion, the only mean of interest to biologists/paleontologists would be the arithmetic mean. The others are more interesting to geometricians or physicists.
Computing the arithmetic means is relatively simple, you sum up all the data points and then you divide by the number of data points. For our list ([2, 12, 12, 19, 19, 20, 20, 20, 25]), that means:
(2 + 12 + 12 + 19 + 19 + 20 + 20 + 20 + 25) / 9 = 16.555
This picture explains everything a bit more clearly:

By Cmglee.
So, 16.555 is the mean, 19 the median, and 20 the mode. Fairly similar numbers, aren't they?
But one question remains, which of these averages is best for categorizing a dataset?
It depends. The mean works only on continuous data while the mode only works for categorical data. The median works for either, so, if you are not sure, it is a safe bet.
Why do we need this? Well, like I said, sometimes, finding out the average of a sample is the whole point. But averages are also the baseline against which the rest of the data can be measured. This helps us identify outliers which might be the result of either inaccurate measurements or statistically improbable events. Usually, it is best to remove such data, as it might falsify our results later. Getting rid of problematic data is also called "clearing" in the field of data science, for those who are interested.
Besides finding the average, we also want to find out how
spread out our data is. This is, again, very significant because, the more spread out our data is, the less of a bearing the average we computed has in the real world.
Considering these two box plots I've found:
 www.statology.org/why-is-standard-deviation-important/
www.statology.org/why-is-standard-deviation-important/The mean is the same for both examples, but company A has clearly far more distribution in its salaries than company B. Therefore, the mean salary is far less informative in company A than in company B.
(Or, to get back to our theropod example: Say you have two species of theropod whose adult mean length is 12 m, but in one species, the range is 10-14 m, but in the other, it's 11-13 m. Same mean, different dispersion.)
Is there a way to describe this kind of dispersion a bit more mathematically? Yes, there is. For continuous data, we have the
variance and the
standard deviation.
For the variance, you take every measurement, subtract the mean from it, square the result (to get rid of negative values), sum everything up, and then divide it by the number of measurements minus 1.
Or you just let a computer calculate it for you, much easier.
Here's an equation, for those who like seeing equations:

In case the image doesn't show, here it is in words:
Variance = SUM((Measurement-Mean)^2) / (n - 1)
N stands for the number of measurements.
For the
standard deviation, you simply form the square root of the variance (or, again, you just let a computer calculate it for you).
Assuming the data are continuous and normally distributed (that is, they are equally likely to be bigger or smaller than the mean), 68% of the data points will be one standard deviation from the mean, 95% will be two standard deviations from the mean (technically 1.96, but I'm rounding), and 99.7% of all data points will be 3 standard deviations from the mean.
It usually looks like this:

The awesome thing is that this applies to lots of population datasets, no matter if it's height or IQ you are measuring.
For example: The mean IQ is 100, the standard deviation is 15. This means that 68% of all individuals have an IQ between 85 and 115, 95% have one between 70 and 130, and so on.
The reason is that there are underlying reasons (e.g. genetics) why a mean exists at all and deviations can happen in either direction with roughly the same likelihood and they become less likely the further you get away from the mean.
If you have a dataset and you aren't sure if it's normally distributed, you can simply make a histogram of it. A histogram is simply a graphical representation of the distribution of a continuous variable and most statistics software should be able to show it. If the distribution you get is bell-shaped, it's normally distributed.
Here's where things get interesting. It's possible to calculate the
standard error by taking the standard deviation and dividing it by the square root of the sample size minus one.
SE = SD/SQR(n-1)
If there is one important thing, it is that your results will
always include an error. This is why people who are good at maths sometimes struggle with statistics. Math doesn't have errors, as it's pure definition. But statistics applies math to the real world. In the real world, your plots never fit neatly on a graph. Instead, you have to find the graph that gets the most hits in this mess we call data.
What the standard error does is that it helps you to determine the confidence interval. The
confidence interval is crucial if you want to extrapolate the findings of your sample on the overall population. For a confidence interval of 95%, simply take the standard error and multiply it by 1.96.
For example: Let's get back to our hundred adult theropods with a mean body length of 12 m. Let's say the standard error you calculated is one meter. 1 * 1.96 is 1.96. That means
you are 95% confident that the
actual mean size of the real species (not just the sample you have) is
somewhere between 10.04 and 13.96 m! Pretty cool, given what small slice of the species you know, isn't it?
(Of course, that assumes that your specimens are representative of all stratigraphic periods and that there aren't any preservation biases at work, but that's a question we'll tackle at the end of this guide.)
A thing to remember,
the bigger the sample size, the more the standard error shrinks! That's why it always pays off to have a sample size as large as possible, even if that's not always easy.
Remember that "study" that tried to "prove" that MMR vaccines cause autism? It had a sample size of only 12 patients!
Don't be like that!
...
Now, I mentioned standard deviations and standard distributions and you might be wondering "Are there also non-standard distributions". Yeah, they are.
For categorical data (Is this animal male or female? Does it have yellow, grey, or black eyes?), there is no mean and thus no standard deviation, no normal distribution, and nothing.
The kind of distribution here depends on the number of outcomes you have. If you only have two outcomes (e.g. is this animal male or female), you have what is called a binomial distribution.
If you have count data (that is, data that starts in zero and that increases up to some point in intervals), you have what is called a Poisson distribution.
They have some fun equations associated with them that can answer questions like "How likely is it that I get 'heads' three times when I flip a fair coin twenty times?". However, I won't waste your time with them because a computer can calculate them far faster than you can by hand.
If you want to know the answer to the coin-flip question, open R and type in the command "dbinom(3, 20, 0.5)". The answer is 0.00108 (0.108%), by the way.
We'll get to probability later, don't worry.
4. Statistical Modelling (or, How To Extrapolate Like a Pro)Okay, enough with that. We have the data, we classified it, characterized it, we even cleaned it up, and we've also done some basic probability calculus.
What we have so far is a good description. But in science, it's not enough to describe things. We also want
predictions.
The problem with our imaginary extinct theropod is that it assumes conditions that are rarely met within the field of paleontology. Imagine a big, cool extinct animal of which we have a hundred complete skeletons of which we know they are adults and which we can measure from snout to tail.
I know, but it's a nice dream.
In more realistic cases, we'll not only have a limited sample size but also limited remains. Consider
O. megalodon. We have thousands of specimens that are only known from isolated teeth. We could calculate its average tooth size, but tooth size by itself isn't a particularly interesting ecological predictor. If there only was a way to derive more ecologically interesting parameters, like total body length, from tooth measurements. Like, if you could create a mathematical model that gives you tooth measurements and calculates the total body size from it.
Oh, wait, that's what this section is about!
Say, you have data (e.g. tooth size and body size). You think there is a relationship between different data variables, but you want to quantify it. What you need is a
regression model.
For any regression model, we need at least two variables, a
dependent and an
independent variable (also called an
explanatory variable in the literature). They are called that way because the dependent variable is thought to depend on other variables (for example, velocity is the product of distance traveled divided by time) while the independent variables can simply be measured (to measure distances, all you need is measuring tape, to measure time, all you need is a stopwatch).
In physics, it's fairly easy to determine if a variable is dependent or independent, as many concepts are explicitly defined as only existing relative to others (velocity is a good example). In biology/paleontology, it is a little a bit different, as it is a less definition-based science. Here, our dependent variable depends on our hypothesis. Here, it is the body length of
O. megalodon, as we can't measure that!
Is there something we can measure? Yes! As mentioned, while postcranial skeletal remains of the megatooth shark are rare, we have teeth. Thousands of them! And we know that their length and width correlate with the size of their owner.
To what extent they correlate is not known. What we can do is we can take an animal in which both values can be obtained with relative ease (say, the modern great white shark) and then determine a relationship.
How do we do this?
Tooth height/width and total length are both fairly continuous variables. If we have an independent and a dependent variable that are both continuous, we use a
simple linear regression, the simples statistical model in existence.
All of you know what a simple linear regression is. It is the kind of model where you put lots of data points in a cartesian coordinate system and then draw a line between them. In a picture:
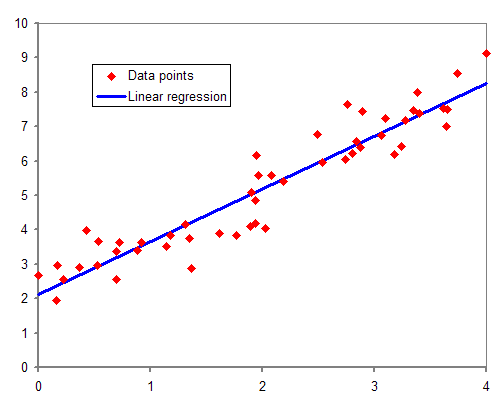
In theory, our undertaking sounds simple. Put the tooth measurements on the x-axis (independent variables always go on the x-axis, that's how it works) and the TL measurements on the y-axis and draw a line.
But how can you make sure that your line hits the maximum number of points?
You'll want an equation that takes the following form:
y = a + bx + e
y and x are the dependent and independent variables, respectively.
a is the intersection between the line and the y-axis.
b is the slope of the line.
e is the error and
we want to get the error as small as possible.
A way of minimizing the error is through the least-squares method. The least squares method calculates the distance between each point and the line and subsequently squares them (this is both to avoid negative values and to smooth out outliers; you already know this from calculating the variance). The smaller e is, the better your line is. You want to find out the line that produces the smallest e. As with most things, statistics software will do this job just fine for you.
...
Since I mentioned simple linear regressions, you might wonder if there are also not-so-simple linear regressions. The answer is: Yes, there are!
If you want to investigate the relationship between body length
and tooth height in a shark, you have a simple linear regression, as you only have two variables.
However, let's assume you are trying to investigate the relationship between tooth height and tooth width on total length. Maybe you think that both correlate with the body length of the animal, but you want to find out which of them is the more significant predictor.
In this case, you have a
multiple linear regression which is a regression where you either have more than one dependent or more than one independent variable. It's not rare to visualize these regressions with three-dimensional coordinate systems.
With statistics software, you can do some cool things. The Python package scikit-learn has a library called linear_model.LinearRegression with which you can take multiple x variables (say, the tooth height and tooth width of a great white shark) and analyze their relationship to a y variable (say, the total body length) to find out which relationship is stronger. (I think you can also do something similar with R's lm() function.)
If it turns out that, for example, the tooth height explains 50% of the length variance, but tooth width explains 58% of the width variance, you should probably use tooth width to build your model for calculating O. megalodon's size!
Note that multiple and simple linear regressions are both intended for normally distributed continuous variables only. If you want to include other types of variables (i.e. categorical variables or variables that are not normally distributed), you need a
generalized linear model (glm). Simply hit "glm()" in R, enter all your variables, and print the result. If you want to learn how this works in detail, you might want to watch an R tutorial.
The software does lots of interesting calculations for you. When you have a regression, one of the most useful variables, in my opinion is that of the
correlation coefficient, which tells you how strong a correlation is. The higher the number, the stronger the (positive) correlation. (And vice versa, a strongly negative number refers to a strongly negative relationship.) A correlation coefficient of 0.2 or lower is negligible. 0.3 is a weak positive correlation[1].
A much simpler way of looking at how strong a correlation is by looking at the slope. How steep is it? How many data points fit it (=how low is the error)? Those are all indicators of how strong a correlation might be.
However, "correlation" is a very good keyword here. Statistical modeling and regression analysis are all about
correlation. However, what we usually want in science is
causation. How do we make the jump from one to the other?
I'm sure you all know what I'm getting at:
5. Why Correlation Does Not Prove CausationYou saw this coming, didn't you? There is no way around a statistics tutorial where this common chestnut isn't going to be addressed.
Statistics have a bit of a bad reputation in the general population for being a tool by the elites used to manipulate the uneducated masses. Even if the data isn't fabricated, it's fairly easy to manipulate.
One of the easiest ways to manipulate data is through insufficient sample sizes, as I already discussed when talking about the standard error.
However, the standard error is only half of the equation. The other half is the
effect size. The effect size is
measuring the extent to which something happened (something like "If I vaccinate this child, how likely is it that it doesn't become sick?"). If your effect size is smaller than your standard error, there's a good chance that whatever correlation you observed is the result of random chance.
How do you prove that your statistical relationship is not the result of random chance? Remember what I said at the beginning about forming hypotheses? Sometimes, the best way to prove something is by disproving its opposite.
So, if you want to prove that your results are statistically meaningful, the
null hypothesis would be a statement of insignificance ("The vaccine has no effect whatsoever on whether the child is healthy or sick").
An important concept in the field of null hypothesis significance testing is the concept of a
p-value. The p-value is the likelihood that you got all your results by chance. If the p-value is below 0.05, it's very unlikely that your results are the result of pure chance, and the null hypothesis is rejected.
Why only then? Why not have the threshold be lower or higher? Well, as it turns out, there can be false positives (false rejections of the null or type I errors) and false negatives (failure to reject the null or type II errors) in statistics. A too-small P will lead to lots of false negatives, a big P means lots of false positives. It seems like history has proven 0.05 to be a sweet spot for most fields. (Remember the 95% confidence interval? That's where this comes from!)
There are many, many tests that you can do to compute statistical significance. ANOVA. T-test. Chi-squared. The programming language R knows many commands to do them for you.
But is a low p-value always good? Not necessarily. While the p-value is related to the standard error and the effect size, a low p-value doesn't always prove there is a significant effect size.
Example: Let's say you have some idiotic medication and the people who take it feel 0.000000001% better than those who don't. This is obviously not statistically significant, but if you did the same test with sample sizes of quadrillions of humans, the difference would still be unlikely to arise by chance and thus have a low p-value.
Please read this for a few moments to let that sink in. This is something PhD students sometimes don't understand. This is something statistics students sometimes don't understand.
It's perfectly possible to have a low p-value and the results might still mean jack.
Why is this misconception so common? Part of the problem lies in the way we use our language. In colloquial usage, the words "probability", "significance", and "likelihood" are all used interchangeably. But for the statistician, each of these words has a clear definition.
I'll try to make it short.
Likelihood = The plausibility of a hypothesis given observed data
Significance = The possibility that we got the data we observed through chance
Probability = A way to quantify likelihood by giving it a number between 0 and 1 (or 0 and 100, if you like percentages).
As I mentioned in the introduction, probability is the end goal of science. But people confuse probability with significance because the latter is easier to calculate.
There are some niche situations where probability is easy to calculate. For example, when you are flipping a fair coin, you are dealing with a Bernoulli distribution and for a binomial distribution, there is a simple formula you can use to calculate the likelihood of a particular result ("e.g. out of twenty fair coin flips, how likely is it to get 'tails' three times"). Please consult Prof. Dr. Wikipedia if you want to see it yourself:
en.wikipedia.org/wiki/Binomial_distribution#Probability_mass_functionSuch a formula is called a
probability mass function. A probability mass function is an excellent solution for problems that have a fairly manageable amount of possible outcomes (e.g. problems involving categorical data). All you need to know is the number of possible outcomes and the number of ways in which a specific outcome can be fulfilled to calculate how likely it is that said specific outcome will be fulfilled.
However, for most scientific problems, there isn't going to be a probability mass function. Ever tried calculating precisely how often a
T. rex is going to beat a
Giganotosaurus in a fight? It aint gonna work.
For most scientific problems, the best way to calculate the likelihood of a hypothesis is through
Bayes theorem. I wrote a post on the theorem in our thread on the Loch Ness Monster:
theworldofanimals.proboards.com/post/47069/threadBayes theorem takes the following form:
P(A/B) = (P(A)*P(B/A))/P(B)
P(A/B) is what we want, the likelihood of the hypothesis (that all swans are white, that Megalodon had a maximum length of 20 m, that T. rex was the biggest theropods, whatever) given the data.
P(A) is the likelihood of the hypothesis before considering any data ("a priori").
P(B/A) is the likelihood of the data given the hypothesis (in other words, this is the p-value)!
P(B) is essentially the sum of P(A)*P(B/A)
for all alternative hypotheses.
If it sounds hard to understand, it's because it is. P(A) is a matter of personal judgment, in most practical cases, there's no way to calculate this parameter. P(B) is near impossible to calculate in most cases, too, because it's always possible that there are hypotheses you are overlooking. (It is possible to calculate all possible phylogenetic trees for a given number of species which is why you sometimes read the words "Bayesian inference" in papers about phylogeny, but I disgress).
For this reason, the vast majority of statistical analysis you will find in the biological literature focuses on P(B/A), the likelihood of the data given the hypothesis, because this can be computed.
But, as we've already covered, a low p-value doesn't necessarily prove a causal relationship. If you need an example:
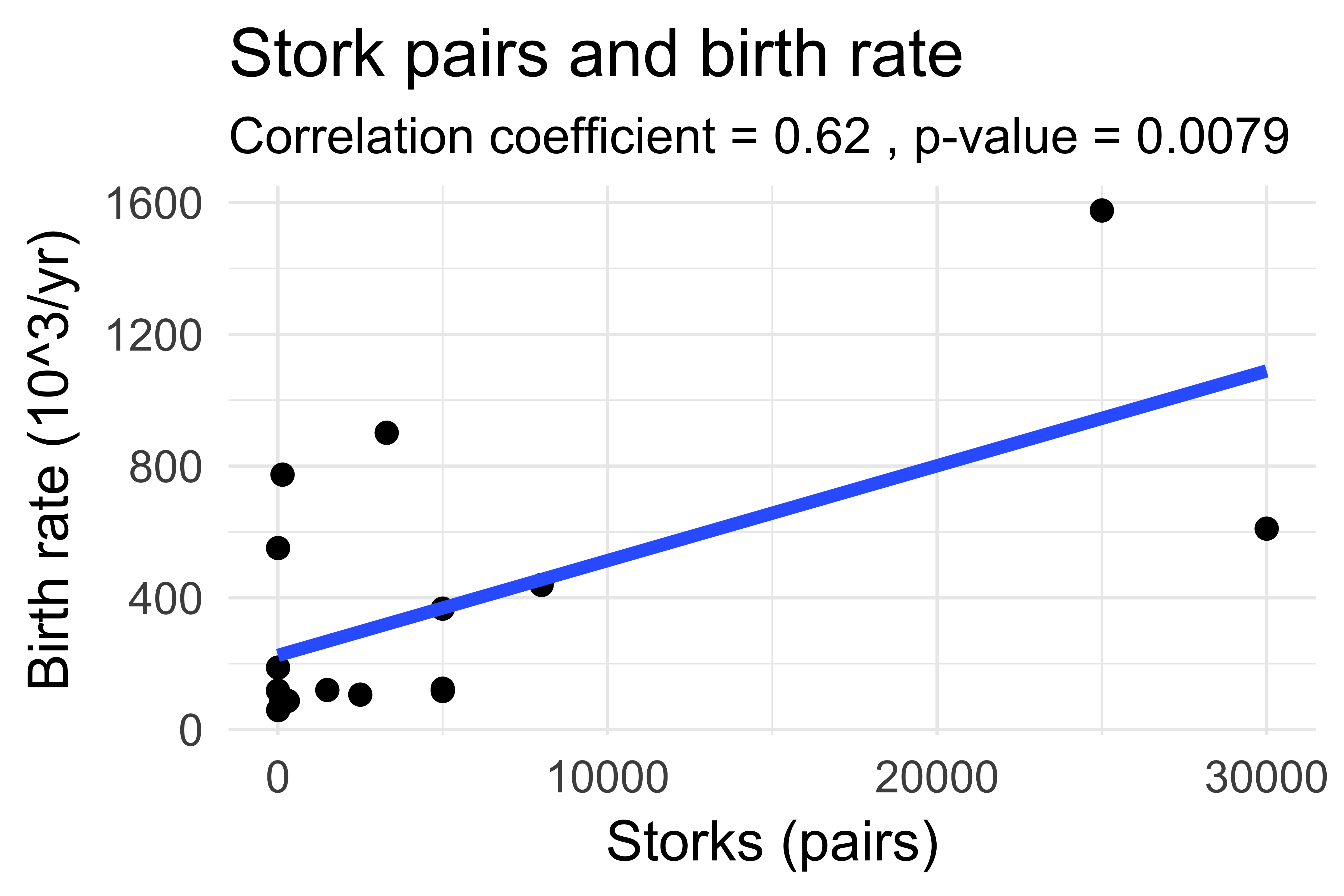
From: Matthews, R. (2000), Storks Deliver Babies (p= 0.008). Teaching Statistics, 22: 36–38.
Countries with lots of storks also have more babies being born and the correlation is statistically significant. However, just because the result is not the product of chance does not mean that storks actually deliver babies. Countries that have lots of storks and lots of babies also have a higher landmass, you know?
A common reason why there sometimes is no causation despite a very significant correlation is because of the presence of a
confounding variable. A confounding variable is defined as a variable that influences both the independent and the dependent variable and thus causes a spurious relationship between the two. Here, the independent variable is the number of storks, the dependent variable is the babies born, and the confounding variable is the landmass size.
In simple terms: Causation is essentially a hypothesis of why there is a correlation. But to "prove" that there is a causation (to the point that you can prove anything in science), you also need to see if there are any other possible causal effects that explain the correlation much better. This is what the variable "P(B)" in the Bayes theorem equation stands for. If P(B) is much higher than all the variables above it, it's unlikely that your hypothesis is true.
So, how do you rule out alternative hypotheses? Maybe by being an expert in your field and having some common sense?
In other words, roughly what you would also do if you didn't know anything about statistics at all.
6. What's the Point of All of This?There is a reason people hate math. Not only is it hard, it's often difficult to see what you need all those calculations for.
If you read the last section, you probably realized that doing the math, by itself, doesn't prove anything (Cameron Pahl, this is for you, please take notes). That's because math, as mentioned several times by now, operates on definition rather than description.
However, math is still invaluable because it provides an objective language through which scientific results can be discussed. Humans are hard-wired to think in absolutes, so if science doesn't prove anything with 100% certainty, why bother with it? But I probably don't need to tell you that it makes a huge difference if a hypothesis has an 89% or a 23% likelihood to be true.
A lot of disagreements people have could easily be dissolved if both sides were willing to formally explain where exactly their disagreement lies, and mathematics prove a very effective language for that.
More practically, statistics provide you with a way to evaluate how good your models are. Ultimately, the goal of science is to build models that can predict future data and to maximize the likelihood of success while minimizing the likelihood of failure. This kind of thinking has brought humanity very far and understanding this will bring you just as far.
And here we already are. As mentioned in the introduction, this guide is focused on introductory subjects, thus topics that I deemed too technical were cut.
If you want to, I can write a follow-up on topics like mixed-effects models (though I'd have to understand that stuff myself first) or hidden Markov models (very important for evolutionary biologists!). I could also write an addendum on statistical software like R and Python and their machine-learning libraries.
That is, if I ever got my time management under control which might never happen.
Citations:
[1] Mukaka MM. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med J. 2012 Sep;24(3):69-71. PMID: 23638278; PMCID: PMC3576830.
General References:
Denis, D. J. (2020). Univariate, bivariate, and multivariate statistics using R: quantitative tools for data analysis and data science. John Wiley & Sons.